Overleg:Shallow water equations

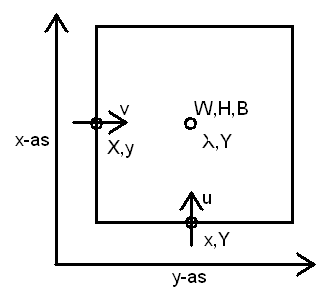
• W = Water
• H = Hoogte, Waterstand
• B = Bodem of Diepte
• u = snelheid in de Noord-Zuid richting
• v = snelheid in de Oost-West richting
• X,Y = midden van een rekencel
• x,Y = onderkant van een rekencel
• X,y = linkerkant van een rekencel

Hoofdletters is het midden van een cel, een kleine letter betekend dat er een halve cel wordt verschoven. Op deze manier zijn snelheden niet in het midden van een cel definieert. Dit heet een staggered grid.

<math> \begin{align} \frac {\partial W_{X,Y}}{\partial t}\cdot DX \cdot DY_X=& u_{x,Y} \cdot W_{x,Y}*DY_{x}-u_{x+1,Y} \cdot W_{x+1,Y} \cdot DY_{x+1}+ \\

                                    & v_{X,y}*W_{X,y}*DX-v_{X,y+1}*W_{X,y+1}*DX

\end{align} </math>

<math> \frac {\partial u_{x,Y}}{\partial t}\cdot DX \cdot DY_x \cdot W_{xY} =impuls_{normaal}+impuls_{tangentieel}+zwaartekracht+kromming+coriolis+getijkracht+frictie </math>

<math> impuls_{normaal}=\frac{1}{2} \codt ({W_{x-1,Y} \cdot u_{x-1,Y}^2 \cdot DY_{x-1} -W_{x+1,Y} \cdot u_{x+1,Y}^2 \cdot DY_{x+1}}) </math>

<math> impuls_{tangentieel}=W_{x,y} \cdot v_{x,y} \cdot u_{x,y} \cdot DX -W_{x,y+1} \cdot v_{x,y+1} \cdot u_{x,y+1} \cdot DX </math>

<math> zwaartekracht=\frac{1}{2} \cdot g \cdot (H_{X-1,Y}-H_{X,Y}) \cdot DY_X \cdot W_{x,Y} </math>

<math> ????kromming=-\frac{u[x][y]}{R}_{aarde}} \cdot DY_X \cdot DX \cdot v_{x,Y}*sin(\theta_x)}???? </math>

<math> coriolis=-2 \cdot \Omega \cdot v_{x,Y} \cdot sin(\theta_x) \cdot W_{x,Y} \cdot DX \cdot DY_x </math>

<math> getijkracht={F_{getij,x}}_{(x,Y)} \cdot W_{x,Y} \cdot DX \cdot DY_x </math>

<math> frictie=-u_{x,Y} \cdot 0.01 \cdot DX \cdot DY_x </math>

<math> \frac {\partial v_{x,Y}}{\partial t}\cdot DX \cdot DY_X \cdot W_{Xy} =impuls_{normaal}+impuls_{tangentieel}+zwaartekracht+kromming+coriolis+getijkracht+frictie </math>

<math> impuls_{normaal}=\frac{1}{2} \codt ({W_{X,y-1} \cdot v_{X,y-1}^2 \cdot DX -W_{X,y+1} \cdot v_{X,y+1}^2 \cdot DX) </math>

<math> impuls_{tangentieel}=W_{x,y} \cdot u_{x,y} \cdot v_{x,y} \cdot DY_x -W_{x+1,y} \cdot u_{x+1,y} \cdot v_{x+1,y} \cdot DY_{x+1} </math>

<math> zwaartekracht=\frac{1}{2} \cdot g \cdot (H_{X,Y}-H_{X,Y-1}) \cdot DX \cdot W_{X,Y} </math>

<math> ????kromming=-\frac{u[x][y]}{R}_{aarde}} \cdot DY_X \cdot DX \cdot v_{x,Y}*sin(\theta_x)}???? </math>

<math> coriolis=-2 \cdot \Omega \cdot u_{X,y} \cdot sin(\theta_X) \cdot W_{X,y} \cdot DY_X \cdot DX </math>

<math> getijkracht={F_{getij,y}}_{(X,y)} \cdot W_{X,y} \cdot DY_X \cdot DX </math>

<math> frictie=-v_{X,y} \cdot 0.01 \cdot DY_X \cdot DX </math>

<math> dwdt[x][y]=u[x][y]*uW[x][y]*dyo[x]-u[x+1][y]*uW[x+1][y]*dyo[x+1]+ (v[x][y]*vW[x][y]-v[x][y+1]*vW[x][y+1])*DX; W[x][y]+=dwdt[x][y]*DT/DX/dym[x];

dudt[x][y]=(uW[x-1][y]*u[x-1][y]*u[x-1][y]*dyo[x-1]-uW[x+1][y]*u[x+1][y]*u[x+1][y]*dyo[x+1])/2.0+ //impuls transport

                  .5*g*(H[x-1][y]-H[x][y])*dyo[x]*uW[x][y]+                                                //potentiele energie

                  ( LOW[x][y]*(v[x][y]+v[x-1][y])*(u[x][y]+u[x][y-1])-                                     
                      ROW[x][y]*(v[x][y+1]+v[x-1][y+1])*(u[x][y+1]+u[x][y]) )/4.0*DX+                      //tangentieel impuls transport

                      -u[x][y]/R*dyo[x]*DX*vopu[x][y]*sino[x]+                                             //curvature

                      -2*omega*vopu[x][y]*sino[x]*uW[x][y]*DX*dyo[x]+                                      //coriolis kracht

                      uGM[x][y]*uW[x][y]*DX*dyo[x]+                                                        //maan getij kracht
                      -u[x][y]*0.01*DX*dyo[x];                                            //frictie

       dvdt[x][y]=(vW[x][y-1]*v[x][y-1]*v[x][y-1]-vW[x][y+1]*v[x][y+1]*v[x][y+1])/2.0*DX+
                  .5*g*(H[x][y-1]-H[x][y])*vW[x][y]*DX+
                  ( LOW[x][y]*(u[x][y]+u[x][y-1])*(v[x][y]+v[x-1][y])*dyo[x]-
                      LBW[x][y]*(u[x+1][y]+u[x+1][y-1])*(v[x+1][y]+v[x][y])*dyo[x+1] )/4.0+   
                      uopv[x][y]/R*dym[x]*DX*uopv[x][y]*sinm[x]+
                      2*omega*uopv[x][y]*sinm[x]*vW[x][y]*DX*dym[x]+
                      vGM[x][y]*vW[x][y]*DX*dym[x]+
                      -v[x][y]*0.01*DX*dym[x];

       dudt[x][y]/=uW[x][y]*DX*dyo[x];
       dvdt[x][y]/=vW[x][y]*DX*dym[x];

</math>