Shallow water equations: verschil tussen versies
| (3 tussenliggende versies door een andere gebruiker niet weergegeven) | |||
| Regel 48: | Regel 48: | ||
|} | |} | ||
Grappig om te zien is dat recht tegenover het fictieve continent een gebied ligt waar helemaal geen getij is. Het gebied herken je | Grappig om te zien is dat recht tegenover het fictieve continent een gebied ligt waar helemaal geen getij is. Het gebied herken je aan het groene ovaaltje rechts boven. | ||
Meer uitleg over het filmpje en het model volgen later. Daarnaast komt er ook toelichting op de navigatie lezing. | Meer uitleg over het filmpje en het model volgen later. Daarnaast komt er ook toelichting op de navigatie lezing. | ||
==Het model== | |||
[[Afbeelding:Cel.png|thumb|360px|left|Een rekencel]] | |||
*'''W''' = Water | |||
*'''H''' = Hoogte, waterstand | |||
*'''B''' = Bodem, diepte | |||
*'''u''' = snelheid in de Noord-Zuid richting | |||
*'''v''' = snelheid in de Oost-West richting | |||
*'''X,Y''' = midden van een rekencel | |||
*'''x,Y''' = onderkant van een rekencel | |||
*'''X,y''' = linkerkant van een rekencel | |||
Hoofdletters is het midden van een cel, een kleine letter betekend dat er een halve cel wordt verschoven. Op deze manier zijn snelheden niet in het midden van een cel definieert. Dit heet een ''staggered grid''. | |||
<math> | |||
H_{X,Y}=W_{X,Y}+B_{X,Y} | |||
</math> | |||
<math> | |||
\begin{align} | |||
\frac {\partial W_{X,Y}}{\partial t}\cdot DX \cdot DY_X=& u_{x,Y} \cdot W_{x,Y}*DY_{x}-u_{x+1,Y} \cdot W_{x+1,Y} \cdot DY_{x+1}+ \\ | |||
& v_{X,y}*W_{X,y}*DX-v_{X,y+1}*W_{X,y+1}*DX | |||
\end{align} | |||
</math> | |||
<math> | |||
\frac {\partial u_{x,Y}}{\partial t}\cdot DX \cdot DY_x \cdot W_{xY} =impuls_{normaal}+impuls_{tangentieel}+zwaartekracht+kromming+coriolis+getijkracht+frictie | |||
</math> | |||
<math> | |||
impuls_{normaal}=\frac{1}{2} \codt ({W_{x-1,Y} \cdot u_{x-1,Y}^2 \cdot DY_{x-1} -W_{x+1,Y} \cdot u_{x+1,Y}^2 \cdot DY_{x+1}}) | |||
</math> | |||
<math> | |||
impuls_{tangentieel}=W_{x,y} \cdot v_{x,y} \cdot u_{x,y} \cdot DX -W_{x,y+1} \cdot v_{x,y+1} \cdot u_{x,y+1} \cdot DX | |||
</math> | |||
<math> | |||
zwaartekracht=\frac{1}{2} \cdot g \cdot (H_{X-1,Y}-H_{X,Y}) \cdot DY_X \cdot W_{x,Y} | |||
</math> | |||
<math> | |||
kromming=-\frac{u_{x,Y}}{R_{aarde}\cdot cos(\theta_x)}} \cdot v_{x,Y}*sin(\theta_x)}\cdot W_{x,Y} \cdot DY_x \cdot DX | |||
</math> | |||
<math> | |||
coriolis=-2 \cdot \Omega \cdot v_{x,Y} \cdot sin(\theta_x) \cdot W_{x,Y} \cdot DX \cdot DY_x | |||
</math> | |||
<math> | |||
getijkracht={F_{getij,x}}_{(x,Y)} \cdot W_{x,Y} \cdot DX \cdot DY_x | |||
</math> | |||
<math> | |||
frictie=-u_{x,Y} \cdot 0.01 \cdot DX \cdot DY_x | |||
</math> | |||
<math> | |||
\frac {\partial v_{x,Y}}{\partial t}\cdot DX \cdot DY_X \cdot W_{Xy} =impuls_{normaal}+impuls_{tangentieel}+zwaartekracht+kromming+coriolis+getijkracht+frictie | |||
</math> | |||
<math> | |||
impuls_{normaal}=\frac{1}{2} \codt ({W_{X,y-1} \cdot v_{X,y-1}^2 \cdot DX -W_{X,y+1} \cdot v_{X,y+1}^2 \cdot DX) | |||
</math> | |||
<math> | |||
impuls_{tangentieel}=W_{x,y} \cdot u_{x,y} \cdot v_{x,y} \cdot DY_x -W_{x+1,y} \cdot u_{x+1,y} \cdot v_{x+1,y} \cdot DY_{x+1} | |||
</math> | |||
<math> | |||
zwaartekracht=\frac{1}{2} \cdot g \cdot (H_{X,Y}-H_{X,Y-1}) \cdot DX \cdot W_{X,Y} | |||
</math> | |||
<math> | |||
kromming=-\frac{v_{X,y}}{R_{aarde}\cdot cos(\theta_X)}} \cdot u_{X,y}*sin(\theta_X)}\cdot W_{X,y} \cdot DY_X \cdot DX | |||
</math> | |||
<math> | |||
coriolis=-2 \cdot \Omega \cdot u_{X,y} \cdot sin(\theta_X) \cdot W_{X,y} \cdot DY_X \cdot DX | |||
</math> | |||
<math> | |||
getijkracht={F_{getij,y}}_{(X,y)} \cdot W_{X,y} \cdot DY_X \cdot DX | |||
</math> | |||
<math> | |||
frictie=-v_{X,y} \cdot 0.01 \cdot DY_X \cdot DX | |||
</math> | |||
Waarin: | |||
<math>DY_{X}=DX \cdot cos(\theta_X}) </math> (DY wordt kleiner naarmate dichter bij de polen) | |||
<math>R_{aarde}=6366707 km</math> (straal van de aarde) | |||
<math>\Omega=-7.27221 \cdot 10^-5 rad/s</math> (rotatiesnelheid van de Aarde) | |||
[[categorie:natuurkunde]] | [[categorie:natuurkunde]] | ||
Huidige versie van 19 mrt 2010 17:44
Aan deze pagina wordt nog gewerkt
Met behulp van Shallow water equations kunnen getijde golven over de oceaan worden uitgerekend. Voorlopige resultaten zijn te zien in een gif filmpje. Je kunt hier nog veel meer leuke plaatjes en animaties verwachten.
| Getij golven over de wereld. |
|---|
 |
 |
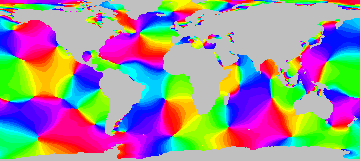 |
In het filmpje zie je duidelijk amfidromisch punten. Dat zijn punten waar geen verval is. Je herkent de punten doordat er altijd een (zwarte) hoogwater lijn naartoe loopt. Bijvoorbeeld een punt recht tussen Brazilië en Kongo. Ook het eiland Madagascar is een amfidromisch punt.
Dijk
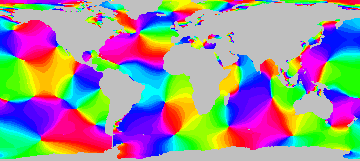
Iemand, ik noem even geen namen, heeft beweerd dat de getijde golf maar op één plek rond de aarde kan stromen. Dat is namelijk rond de zuidpool, ten zuiden van Argentinië, Australië en Zuid-Afrika. Daarom ontstaat daar het getij. Dat verhaal wordt met onderstaande simulaties ontkracht. Omdat ook met de dijk er gewoon getij ontstaat.
Naast de werkelijke wereld staat hier onder een simulatie waarin een er een dijk is gebouwd tussen Vuurland (Zuid-Argentinië) en Antarctica. Opvallend is dat de resultaten eigenlijk nauwelijks verschillen. Lokaal aldaar zijn er wel kleine verschillen, maar over de rest van de wereld veranderd er niets aan de getijde karakteristieken. Beide gevallen zijn hieronder samen afgebeeld als animatie, vervalkaart en fasekaart.
| Getij golven over de wereld. | Getij golven met dijk tussen Vuurland en Antarctica. |
|---|---|
 |
 |
 |
 |
 |
 |
Fictieve situatie
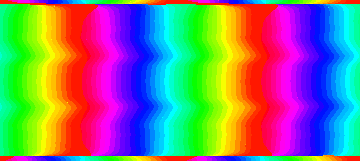
Er is twee keer per dag hoogwater, omdat de krachten die maan veroorzaakt aan de zijde van de maan precies hetzelfde zijn aan de achterzijde van de aarde. Eigenlijk zou je dan verwachten dat de getijde golf netjes met de maan meebeweegt. Dit zou ook het geval zijn als er geen continenten zijn en de oceaan overal even diep. Gelukkig kan deze fictieve situatie eenvoudig worden gesimuleerd. Je ziet dat er slechts een beetje verval is rond de evenaar en verder eigenlijk nauwelijks.
Continenten hebben een enorme invloed op het getij. Als er één fictief continent in de oceaan zou liggen dan ontstaan er amfidromisch punten gebieden met veel meer verval en een het patroon wordt zeer chaotisch.
| Getij golven voor een lege oceaan van 5km diep | 5km diepte oceaan met één fictief continent |
|---|---|
 |
 |
 |
 |
 |
 |
Grappig om te zien is dat recht tegenover het fictieve continent een gebied ligt waar helemaal geen getij is. Het gebied herken je aan het groene ovaaltje rechts boven.
Meer uitleg over het filmpje en het model volgen later. Daarnaast komt er ook toelichting op de navigatie lezing.
Het model
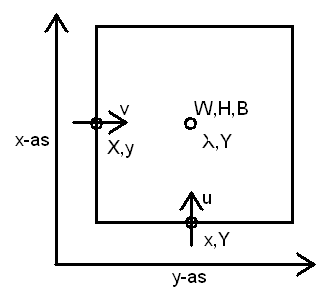
- W = Water
- H = Hoogte, waterstand
- B = Bodem, diepte
- u = snelheid in de Noord-Zuid richting
- v = snelheid in de Oost-West richting
- X,Y = midden van een rekencel
- x,Y = onderkant van een rekencel
- X,y = linkerkant van een rekencel
Hoofdletters is het midden van een cel, een kleine letter betekend dat er een halve cel wordt verschoven. Op deze manier zijn snelheden niet in het midden van een cel definieert. Dit heet een staggered grid.
Fout bij het parsen (onbekende functie "\codt"): {\displaystyle impuls_{normaal}=\frac{1}{2} \codt ({W_{x-1,Y} \cdot u_{x-1,Y}^2 \cdot DY_{x-1} -W_{x+1,Y} \cdot u_{x+1,Y}^2 \cdot DY_{x+1}}) }
Fout bij het parsen (syntactische fout): {\displaystyle kromming=-\frac{u_{x,Y}}{R_{aarde}\cdot cos(\theta_x)}} \cdot v_{x,Y}*sin(\theta_x)}\cdot W_{x,Y} \cdot DY_x \cdot DX }
Fout bij het parsen (onbekende functie "\codt"): {\displaystyle impuls_{normaal}=\frac{1}{2} \codt ({W_{X,y-1} \cdot v_{X,y-1}^2 \cdot DX -W_{X,y+1} \cdot v_{X,y+1}^2 \cdot DX) }
Fout bij het parsen (syntactische fout): {\displaystyle kromming=-\frac{v_{X,y}}{R_{aarde}\cdot cos(\theta_X)}} \cdot u_{X,y}*sin(\theta_X)}\cdot W_{X,y} \cdot DY_X \cdot DX }
Waarin:
Fout bij het parsen (syntactische fout): {\displaystyle DY_{X}=DX \cdot cos(\theta_X}) } (DY wordt kleiner naarmate dichter bij de polen)
(straal van de aarde)
(rotatiesnelheid van de Aarde)